Part I | Part II →
This is the first post of a two-part series exploring the measurements of distances to celestial objects, starting in this post with the methods Ancient Greek astronomers used to measure the distance to the Sun based solely on naked-eye observations and some creative geometry.
Introduction
The first estimation of the Earth-Sun distance, which I’ll denote \(d_\odot \) (where \( \odot \) is the symbol for the Sun) was conducted by Aristarchus of Samos in a work titled On the Sizes and Distances. In it he ultimately calculated the distance to both the Sun and Moon in terms of the solar radius, lunar radius and the radius of the Earth. Thankfully, another Greek polymath by the name of Eratosthenes (who you might have heard of had you ever needed to rapidly calculate prime numbers) had estimated the circumference of the Earth via observing the shadows cast off a rod of a known length. Thus Aristarchus knew the radius of the Earth, but the radius of the Moon or the radius of the Sun remained out of reach. Luckily, this didn’t actually matter, because it just so happens that the Moon and Sun have almost exactly the same apparent angular size in the sky. This enabled Aristarchus to simply equate the ratio of their radii to the radio of their distances via similar triangles. This fortuitous arrangement is often cited as enabling the remarkable progress of astronomy in the classical world. So, a natural follow-up question is what if the Moon did not have the same angular size as the Sun? That is the question we aim to answer. Firstly, let’s start right from scratch and measure the radius of the Earth.
A gnomonic conjecture
Eratosthenes’ original work describing his method of calculating the circumference of the Earth is lost to the ages. Instead, the accepted tale is based off Cleomedes‘ On the Circular Motions of the Celestial Bodies. Consider two observers, one in Alexandria, the other in Syrene (modern Aswan), both cities in Ptolemaic Egypt. They each observe a sundial consisting of a vertical gnomon with known height \( h \) at 12pm on the summer solstice. At this time, the Sun is directly overhead in Syrene; the gnomon casts no shadow. In Alexandria, however, the gnomon casts a shadow of length \( s \).
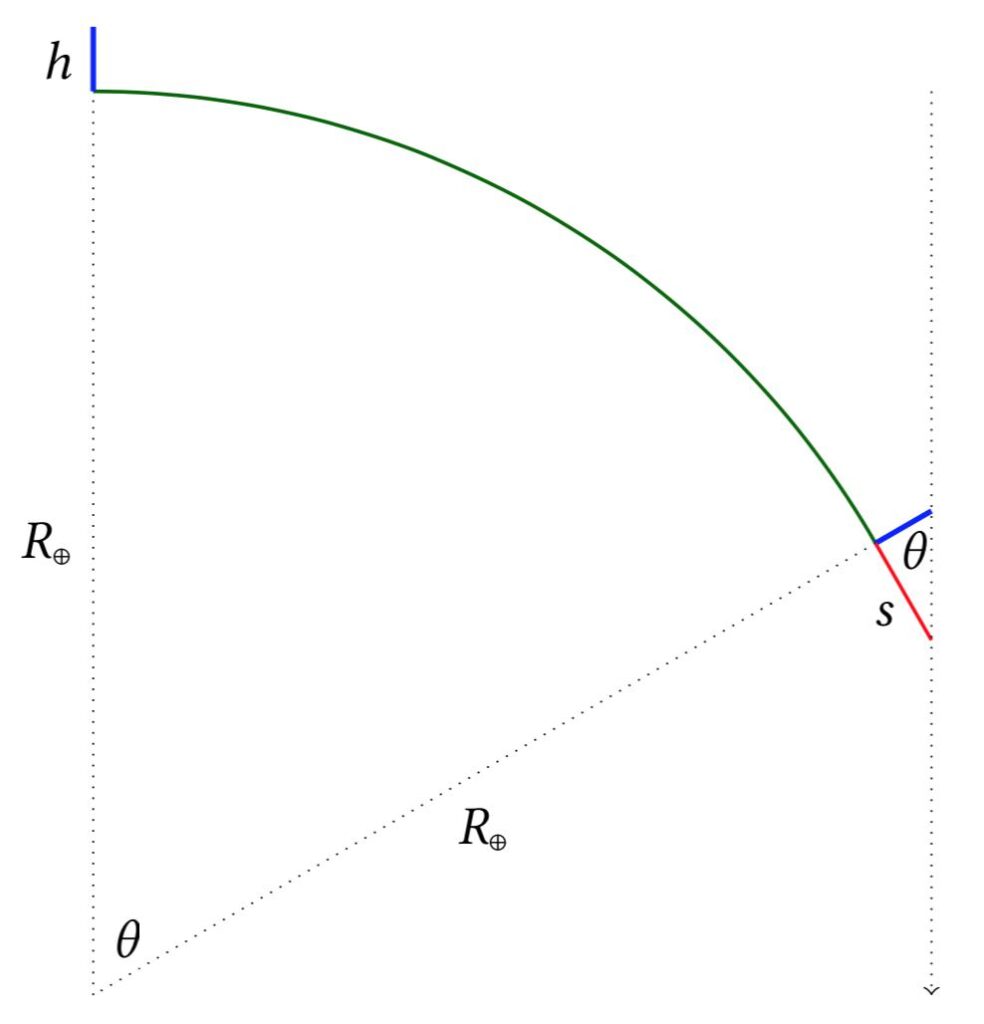
Thus we know the angle is just \[ \tan^{-1} (s/h) \] and so the circumference of the Earth, \( c_\oplus \) is \[ c_\oplus = \frac{2\pi}{\tan^{-1} (s/h)} d_c \] where \( d_c \) is the distance between the two cities and the symbol \( \oplus \) is the (astronomy) symbol for the Earth. Of course we can also just directly obtain the radius of the Earth, \( R_\oplus \), from the arc-length \[ R_\oplus = \frac{d_c}{\tan^{-1}(s/h)} \quad \left( \equiv \frac{c_\oplus}{2\pi} \right) \] It should be noted for these formulae that all angles are in their natural unit of radians, not degrees. There are some caveats with this method. In general, the distance term \( d_c \) really should be the north-south (latitudinal) distance between any two cities. Alexandria is slightly to the west of Syrene. Furthermore, this method seems to rely on knowing the distance to a city in which the Sun shines directly overhead for at least one day of the year. This means one of the cities must be between the Tropic of Cancer and Tropic of Capricorn. While the ancient Britons built structures that could accurately mark the solstices, they could not measure the circumference of the Earth… or could they?
Must the Sun really be overhead one of the cities?
No. There is nothing to stop us from just comparing the lengths of two different shadows, which can be done on any day of the year rather than just on the summer solstice. Let’s imagine a gnomon of height \( h_1 \) casts a shadow of length \( s_1 \) in one city, and a gnomon of height \( h_2 \) casts a shadow of length \( s_2 \) in another city with a higher latitude. The two cities are separated by a north-south distance of \( d \). The angles formed by these shadows are all relative to the Sun’s rays, which we assume are parallel across the entire surface of the Earth (as the diagram to the right illustrates).
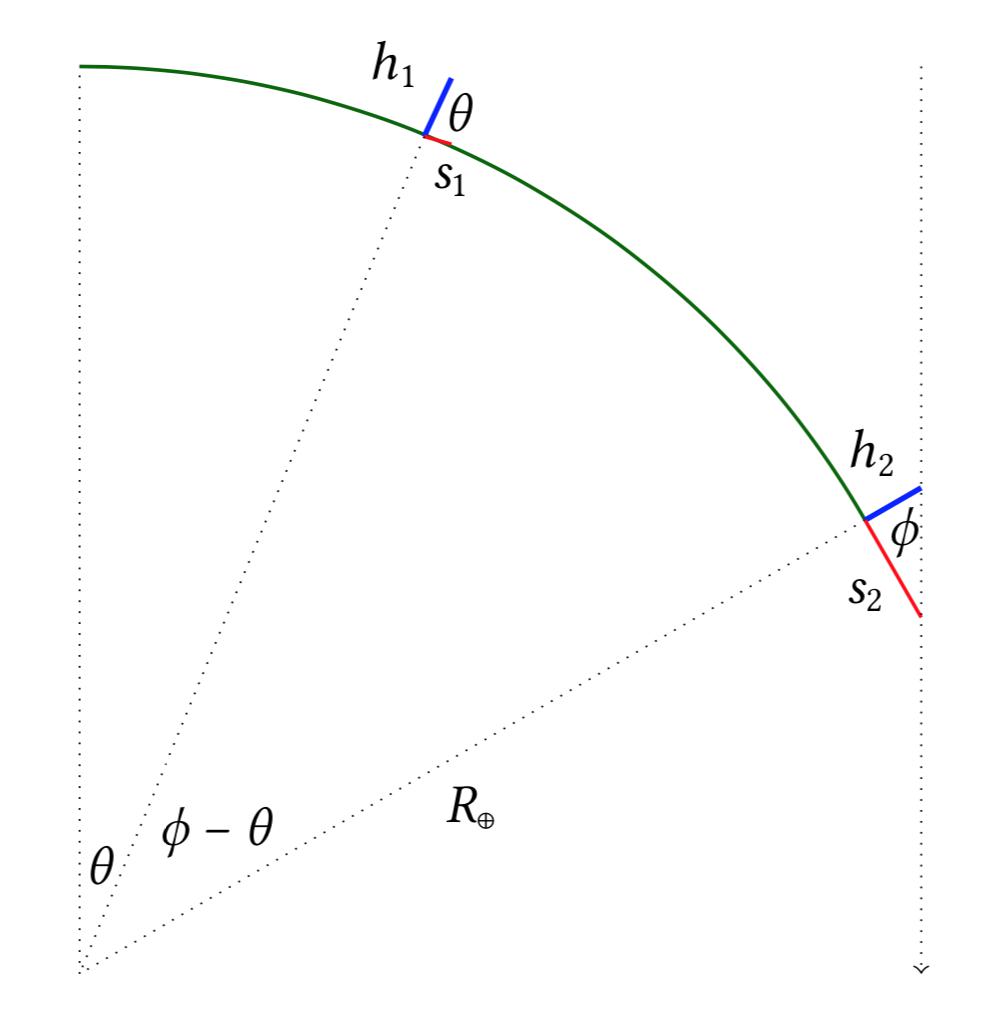
In this case, the radius of the Earth is just \[ R_\oplus = \frac{d}{\tan^{-1}(s_2 / h_2)-\tan^{-1} (s_1 / h_1) } \] where, as before, we’re simply using the formula for arc length. So yes, it is definitely possible to calculate the radius of the Earth without necessarily needing the Sun to be directly overhead one of the cities, so long as there are at least two shadows to compare.
Do it yourself!
You can measure Earth’s radius in your own backyard with just one shadow cast off a single stick. There is a catch though: you can only do this twice a year during the equinoxes (as the Sun is over the equator). Simply take a stick or rod or something with a known length and place it upright on some sufficiently level surface. Wait till 12pm (or whenever the Sun is at its maximum elevation, your local time may vary), then measure the length of the shadow. Next, go to Google Maps and measure the distance from your home to the equator. Now just plug in your numbers and calculate \[ R_\oplus = \frac{\text{distance to equator}}{\tan^{-1} (s / h)} \] Finally it’s important to keep in mind that the major assumption underlying Eratosthenes’ method is that the Earth is perfectly spherical. This is not the case, although the difference between the equatorial and polar radius is around 0.3% and can, for the rest of this post, be ignored.
The power of the half-moon
Having now obtained \( R_\oplus \), the next step is to establish some geometric relations based on our observations of the Sun and the Moon. Perhaps the most obvious is to observe the lunar phases. Since the invention of the calendar, various civilisations have relied on the lunar cycle to tell time, mark significant cultural or religious festivals (e.g. Chinese New Year, Easter, etc.) and plan harvests. Yet the lunar phase can also tell us something important: the ratio of the distance to the Sun \( d_\odot \) and the distance to the Moon \( d_M \).
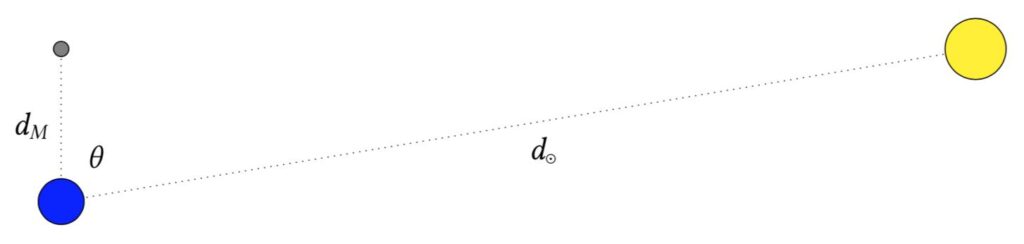
Consider a half-moon, i.e. the first and last quarter phases. During this time, the Earth, Moon and Sun form the vertices of a right-angled triangle where the distance to the Sun is its hypotenuse. If the Moon and Sun are separated by an angle of \( \theta \), then it follows that \[ \frac{d_\odot}{d_M} = \frac{1}{\cos\theta} \] Aristarchus estimated this angle at around \( 87^\circ \), which implies a distance ratio of around \( d_\odot / d_M \approx 19 \). Of course, we now know that the Sun is way further out than that. A more accurate value of around \( 89.85^\circ \) yields a ratio of \( d_\odot / d_M \approx 382 \).
The Solar Eclipse
Now that we know a ratio of distances, how can we relate this to a ratio of radii? Observing a total solar eclipse – in particular, how the Moon and Sun appear to be the same size and line up exactly – allows us to draw the following triangle:
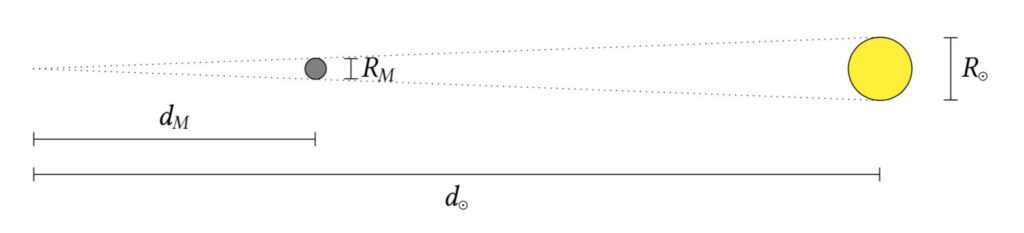
This implies that \[ \frac{d_\odot}{d_M} = \frac{R_\odot}{R_M} \] where \( R_\odot \) and \( R_M \) are the radius of the Sun and Moon respectively. Let’s park our “what if the Moon wasn’t the same size” question for now, and instead complete Aristarchus’ original method.
Earth’s shadow
There’s another incredibly useful source of information; lunar eclipses. Not only are they more common than total solar eclipses, they can reveal some important information based on how they interact with Earth’s umbral shadow. We can measure the radius of the shadow, \( r_{\text{umbra}} \), in terms of some multiple \( n \) of the radius of the Moon \( R_M \), i.e. \[ r_{\text{umbra}} = n R_M \] Aristarchus estimated the radius of Earth’s shadow (at the distance of the Moon) to be approximately 2 moon radii, but modern estimates have this closer to around 2.5.
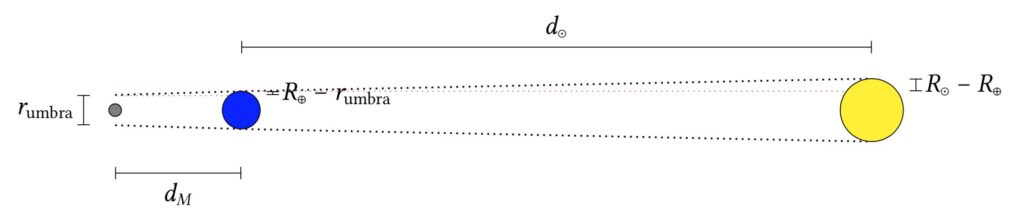
Let’s now replicate Aristarchus’ full construction that involves yet another pair of similar triangles. We have \[ \frac{d_\odot}{d_M} = \frac{R_\odot – R_\oplus}{R_\oplus – nR_M} \] From observing the solar eclipse we established that \[ \frac{R_\odot}{R_M} = \frac{d_\odot}{d_M} = \delta \] where \( \delta \) is the numerical value obtained from the Moon-Sun angular separation. This means that we can express the radius of the Sun \( R_\odot \) in terms of the radius of the Earth \( R_\oplus \): \[ R_\odot = \frac{\delta + 1}{n + 1} R_\oplus \] and the radius of the Moon \( R_M \) in terms of \( R_\oplus \): \[R_M = \frac{\delta + 1}{\delta (n + 1)} R_\oplus = \frac{R_\odot}{\delta} \] Plugging in \( n = 2.5 \) and \( \delta = 382 \), we find \[ R_\odot \approx 109 R_\oplus \quad R_M \approx 0.285 R_\oplus \] i.e, the Sun’s radius is 109 times that of Earth, and the Moon’s radius is only 28.5% that of Earth’s.
The Sun’s angular size
We were able to calculate the radius of the Sun and Moon in terms of Earth radii thanks to knowing the value of the ratio of the solar and lunar radii, and knowing that this ratio of radii is equal to the ratio of distances. This unfortunately still doesn’t tell us distance, but we can find this easily by considering the Sun’s angular size.
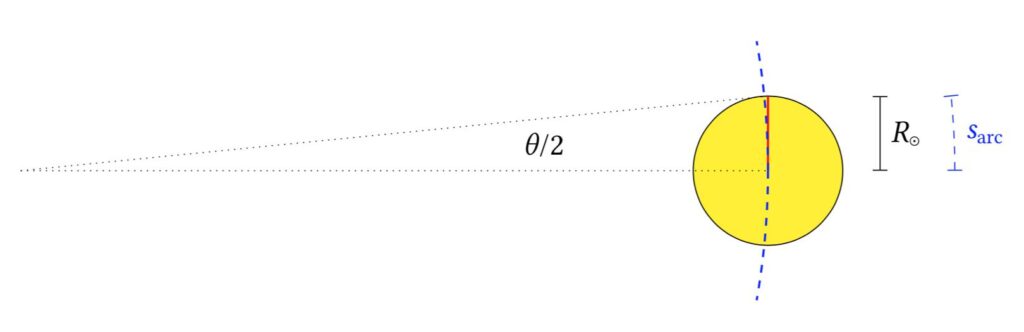
Modern measurements show that the Sun’s angular diameter is around \( 0.52^\circ \). Assuming that the curved arc length \( s_{\text{arc}} \) is roughly equal to the straight-line radius \( R_\odot \) (see above figure), we can establish that \begin{align*} d_\odot = \frac{109 R_\oplus}{\tan(\theta / 2)} \quad \boxed{\approx 24000R_\oplus} \end{align*} If this assumption seems too far-fetched, consider instead the formula for chord length: \begin{align*} R_\odot = d_\odot \sin(\theta/2) \to d_\odot = \frac{109 R_\oplus}{\sin(\theta / 2)} \approx 24000R_\oplus \end{align*} This gives a fairly identical answer, which is to be expected given the small angle approximation \( \sin(\theta) \approx \tan(\theta) \approx \theta \) for \( \theta \ll 1 \) radian.
So just how accurate is Aristarchus’ method?
To determine the absolute best precision of Aristarchus’ purely geometric method, let’s use the modern value of \( R_\oplus = 6378 \) km.
| Quantity | Calculated value (km) | Accepted value (km) | Error |
| \( R_\odot \) | \( 6.952 \times 10^5 \) | \( 6.963 \times 10^5 \) | 1.634% |
| \( d_\odot \) | \( 1.531 \times 10^8 \) | \( 1.496 \times 10^8 \) | 2.321% |
| \( R_M \) | \( 1.818 \times 10^3 \) | \( 1.737 \times 10^3 \) | 4.648% |
| \( d_M \) | \( 4.007 \times 10^5 \) | \( 3.844 \times 10^5 \) | 4.244% |
So from pure geometry, we can obtain the distance to the Sun within 2.3% of its true value. This is quite remarkable considering this method assumes that:
- The Earth and Sun are perfectly spherical (both are slightly bulged at the equator)
- The Moon’s orbit around the Earth is circular (it is not, its eccentricity is around 0.0549)
- The Earth’s orbit around the Sun is circular (its eccentricity is around 0.0167)
- The Earth, Moon and Sun are on the same orbital plane (Earth’s orbit is inclined by around \(7^\circ\))
What if we couldn’t observe a total eclipse?
In other words, what if the Moon did not have the same angular size as the Sun? It would appear that Aristarchus’ entire construction is contingent on the Moon and Sun having the same angular size in the sky. This is so that we can equate the ratio of their radii with the ratio of their distances. Does this mean that only a civilisation birthed on a planet with a moon capable of undergoing a total eclipse with its parent star is able to calculate the distance to its sun? Brilliant.org’s lesson on this topic claims that Aristarchus’ calculation would otherwise have been “upended by too many unknowns” and questions whether humanity’s progress would have been “stunted” were we on a different planet.
Let’s consider a world which is not so lucky; a world in which we could only ever observe annular eclipses, (i.e this world’s moon has a smaller angular diameter than its sun). Assuming that we can still measure \( d_\odot / d_M \) using the quarter-phase angular separation, is it still possible to find some sort of relation between \( d_\odot / d_M \) and \( r_\odot / r_M \)? I argue yes.
A ratio of angular sizes
Suppose this alien sun has an angular diameter of \( \theta \) and the moon has an angular diameter of \( \phi \). Given that we are considering annular eclipses, this means that \( \theta > \phi \).

The triangles in the diagram are not similar triangles… but they are still triangles, and so we can still apply some right-angled trigonometry (assuming, like before, that the curved arc length \( \approx \) the straight-line radius) to deduce that \[ R_M = d_M \tan(\phi/2) \quad R_\odot = d_\odot \tan(\theta/2) \] So, we end up with the relation \[ \frac{R_\odot}{R_M} = \frac{d_\odot}{d_M}\left(\frac{\tan(\theta / 2)}{\tan(\phi / 2)}\right) = \frac{d_\odot}{d_M} \rho \] where we’ve used the shorthand \( \rho = \tan(\theta / 2) / \tan(\phi / 2) \). The distance ratio is thus simply \[ \frac{d_\odot}{d_M} = \frac{R_\odot}{R_M}\left(\frac{\tan(\phi / 2)}{\tan(\theta / 2)}\right) = \frac{1}{\rho}\frac{R_\odot}{R_M}\]
An extra factor
So long as we are still able to accurately calculate the angle between the quarter-phase, half-moon and the sun, we will be able to estimate the distance ratio \( d_\odot / d_M = \delta \). Similarly, so long as we can observe lunar eclipses, we can apply Aristarchus’ similar triangles find a relationship between \( R_\odot, R_M \) and \( R_\oplus \). And finally, we will be able to explicitly calculate \( d_\odot \) through measuring the sun’s angular diameter \( \theta \). All that will change is this extra factor of \( \rho \). Because we know the ratio of angular sizes, it doesn’t matter if this moon is further away or smaller. Since \( R_\odot / R_M = \rho \delta \) we have that \[ R_\odot = \frac{\delta + 1}{1 + n/\rho}R_\oplus \quad \quad R_M = \frac{\delta + 1}{\delta (n + \rho)} R_\oplus \] and so the distance to the sun \( d_\odot \) is simply \begin{align*} d_\odot &= \frac{\rho}{\tan(\theta/2)}\left(\frac{\delta + 1}{n+\rho}\right) R_\oplus \\ &= \boxed{ \frac{1}{\tan(\phi/2)}\left(\frac{\delta + 1}{n+\rho}\right) R_\oplus } \end{align*}
In conclusion, the Sun and the Moon do not have to be the same size in the sky. A society on this planet would still be able to calculate the distance to its sun. The claim that this calculation would otherwise be “upended by too many unknowns” simply doesn’t stack up. That said, it is a happy coincidence that, for our planet, \( \rho = 1 \).
What’s Next
The next Measuring the Sky instalment will cover the concepts of parallax and transit timings, and with these the ability to estimate the distances to other planets. It will also discuss the Copernican Revolution, Galileo’s discoveries and Kepler’s laws of planetary motion.

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
Wikipedia articles:
Inspiration also taken from Brilliant.org’s “Greek Estimates” lesson, part of the Astrophysics course (premium subscriber only).
All diagrams are original, produced with TikZ/LaTeX.