Measuring the Sky II: Models, Planets and Transits

Welcome to the second post in the Measuring the Sky series. Here we follow on from the first post and start to look at distances to the planets, and how planetary transits can be used to measure the distance to the Sun. We’ll start off with a historical interlude and cover the transition from geocentrism to heliocentrism, culminating in the discovery of Kepler’s laws of planetary motion. Next, we’ll look at how to estimate the distance to the planets using geometry, then conclude with the historically significant Transit of Venus.

Parallax

Let’s begin with the concept of parallax, i.e. the “shift” in an object’s position – relative to some static background – when an object is observed from two different directions. The earliest application of parallax to astronomy was performed by the Greek astronomer Hipparchus to estimate the distance to the Moon in terms of Earth radii. Hipparchus’ method involved observing a solar eclipse from two different cities – one under the path of totality, the other outside (and thus only able to observe a partial eclipse). It is also possible to measure the lunar parallax simply by observing the Moon’s change in position when viewed from a different places on Earth (relative to background stars). We will circle back to parallax later in this post (and again in Part IV of this series), but for now let’s lay some groundwork with a brief sojourn through the history of astronomy.

The centre of the Universe

Throughout much of history, starting with Aristotelian physics and standardised with Ptolemy, the prevailing worldview of our place within the Universe was geocentrism. As the name suggests, this model places the Earth at the centre of the Universe, with all celestial bodies, including the Sun and stars, orbiting around the Earth. This model stemmed predominantly from Greek philosophy – itself a byproduct of early Jewish and Mesopotamian mythology – which asserted that Earth is a flat disc suspended in a vast, primordial cosmic ocean, with the firmament acting as a dome over the Earth, dividing the waters above from the dry land below. As an aside, many ancient cultures include floods in their creation myths. The biblical flood in the story of Noah (itself closely related to the Babylonian Epic of Gilgamesh) is asserted to have occurred when both the springs of the deep and floodgates of heaven were opened, thus letting in the waters from this cosmic ocean. The planets, Sun, Moon and stars all orbit within this dome at various heights.

The Ptolemaic model remained entrenched for millennia. Yet that is not to say alternative models did not exist in ancient times. Aristarchus was the first to propose a heliocentric model of the Universe – a model which asserted that it was the Earth in orbit around the Sun, and not the other way around, however it would be well over a thousand years before heliocentrism made a comeback. Copernicus proposed a heliocentric model in 1543 – a pivotal event in ushering forth the broader Scientific Revolution – however the study and promulgation of this model remained forcibly suppressed throughout much of the late 16th to early 17th century. After the Ninety-Five Theses were nailed onto a church door, the Roman Catholic church felt the need to reassert itself. Naturally, anything that questioned the divine order of things would eventually draw the ire of the inquisition. This culminated in events including the famous trial of Galileo and the lesser-known burning-at-the-stake of Bruno. All the major powers of Europe at the time of these events were embroiled in a wider Protestant vs. Catholic (or rather, the Habsburgs vs. everyone else) struggle where religious tolerance (or academic freedom for that matter) was nonexistent. Nevertheless, such is the lasting legacy of religious fundamentalism, coupled with modern-day pseudoscience, that even today people still believe that the Sun revolves around the Earth, or that the Earth is flat and rests atop a turtle. Let’s quickly go through the main geocentric and heliocentric models, as well as one man’s attempt to split the middle.

Gears of Heaven

On the one side lay the prevailing Ptolemaic model of geocentrism, on the other lay the heretical Copernican model of heliocentrism. The Ptolemaic model was rather unwieldy when it came to describing the motion of the planets. Each planet was described by two circles; a deferent and an epicycle. The deferent can be thought of as an offset such that the centre of the circle, marked by an X in the diagram to the right, is away from the Earth. The epicycle is a much smaller circle that was added in order to explain the retrograde motion of certain planets. In this system, planets orbit along the epicycle, which itself revolves around the deferent.

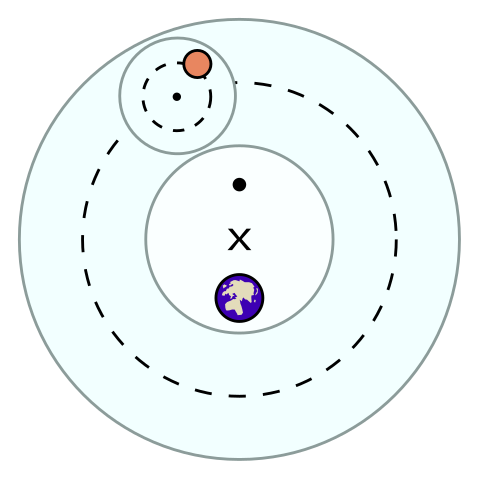
The Copernican model, by contrast, uses only a single circle for the orbit of each planet (though it would later be found that these orbits are actually ellipses). Here all planets orbit around the Sun. Notably, this model easily explains retrograde motion via the relative motion of the Earth along its orbit. Yet although this model was far cleaner and elegant, adopting it required a titanic shift in ideology that few were willing to completely accept.

One famous astronomer who objected to a heliocentric model on theological grounds, yet was prepared to draw inspiration from it, was Tycho Brahe. Most known for his incredibly detailed observations, Brahe sought to combine the mathematical advantages of the Copernican model within a model where Earth was still the centre. The model he developed is called the Tychonic system. Brahe reasoned that the Earth’s natural state ought to be at rest rather than in motion. In Brahe’s model, the planets orbit the Sun, and the Sun orbits the Earth. At its heart, this is a geocentric model, albeit with the other planets orbiting the Sun.

A sense of proportion

Ironically, another big reason why Tycho Brahe was so adamant that the Earth stands still was that he did not observe any stellar parallax. Brahe reasoned that, if the Earth were to orbit the Sun, then the stars should show signs of parallax when the Earth is at opposite ends of its orbit. Of course, the stars actually do show signs of stellar parallax: it’s part of the definition of the parsec, the primary distance measure in astronomy. However, 16th century telescopes simply weren’t powerful enough to measure such tiny parallaxes. Furthermore, no one at the time understood just how far away the stars were. The stars were thought to be just another sphere of heaven. The Arabian astronomer al-Urdi estimated the distance to the sphere of stars as some 140,000 Earth radii (about \( 8.94 \times 10^8 \) km, or around 6 astronomical units (AU), 15% further than the orbit of Jupiter around the Sun). Other medieval estimates put this distance at less than 1 AU! The distance to our nearest star other than the Sun is around 4.25 light years, which is around 45,000 times further away than the largest estimate at the time. No wonder Tycho Brahe found it odd that he couldn’t observe any significant stellar parallax.

And yet it moves

Galileo Galilei, hailed as the father of modern physics, observed two crucial pieces of evidence that shattered geocentrism to its core. As expected, this crucial evidence was flat out denounced by the usual suspects. But for those who thought that banning books they deemed heretical would somehow alter the Laws of Physics, Galileo would, in the end, be proven completely right. The first of these discoveries, made in 1610, were the Galilean moons, Jupiters’ four largest: Io, Europa, Ganymede and Callisto. Initially thought to be stars, Galileo realised these were moons after observing an occultation (i.e. one of the moons went behind Jupiter). This seemed to contradict the notion that all celestial bodies ought to orbit the Earth. The second and more conclusive piece of evidence Galileo found were the phases of Venus. In particular, Venus exhibited a full set of phases, and seemed to appear bigger in its “crescent” phase while smaller in its full / “gibbous” phase, something which is not possible in a geocentric model. Thus Venus had to be orbiting the Sun.

Distance to inferior planets

How we can we estimate the distance of Venus’ orbit around the Sun using only basic trigonometry? We’ll go over a very simple method – one readily available to Johannes Kepler – which involves measuring the angle of greatest elongation. Venus is an inferior planet: this means its orbit lies inside that of the Earth’s. As such, from the point of view of the Earth, Venus will reach a point in the sky where it is furtherest from the Sun. This is known as the point of greatest elongation. There are two such points; the greatest eastern and greatest western elongation. This is why Venus can be both the morning star and evening star (so too Mercury although it is not as easily visible). All we need to measure Venus’ distance from the Sun is an estimate of Earth’s distance from the Sun, and the angle between Venus and the Sun during Venus’ greatest elongation. There’s nothing special about Venus: this method can be used for all inferior planets.

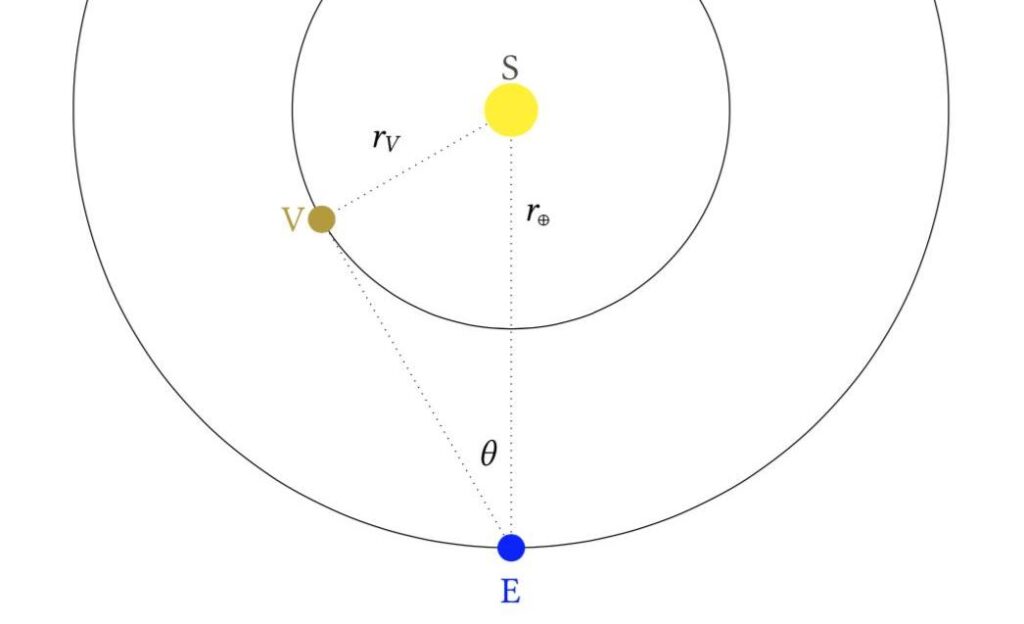
If we measure the angle of greatest elongation (angle SEV) to be \( \theta \), then \[ r_V = r_\oplus \sin(\theta) \] This is since the triangle formed at greatest elongation is right-angled. You can also think of greatest elongation as the time when the tangent line at Venus’ orbital position intersects the Earth.

Distance to superior planets

Can we use a similar method to find the distance to planets like Mars – superior planets that orbit beyond Earth’s orbit? Yes. After all, it ultimately it boils down to the same right-angled triangle as in the previous figure, but we need some extra information. In order to construct an appropriate triangle, we need to know the synodic period of the superior planet. This is the time it takes for the planet to return to the same position in its orbit; this can be easily measured by determining the time between two successive oppositions. Then, we need to know the time \( t \) between that planet’s opposition (i.e the point at which it is opposite the Sun) and quadrature (when the angle between the planet and Sun, as viewed from earth, is 90 degrees). Let’s see how this works with the following figure, using the Earth and Mars as examples.

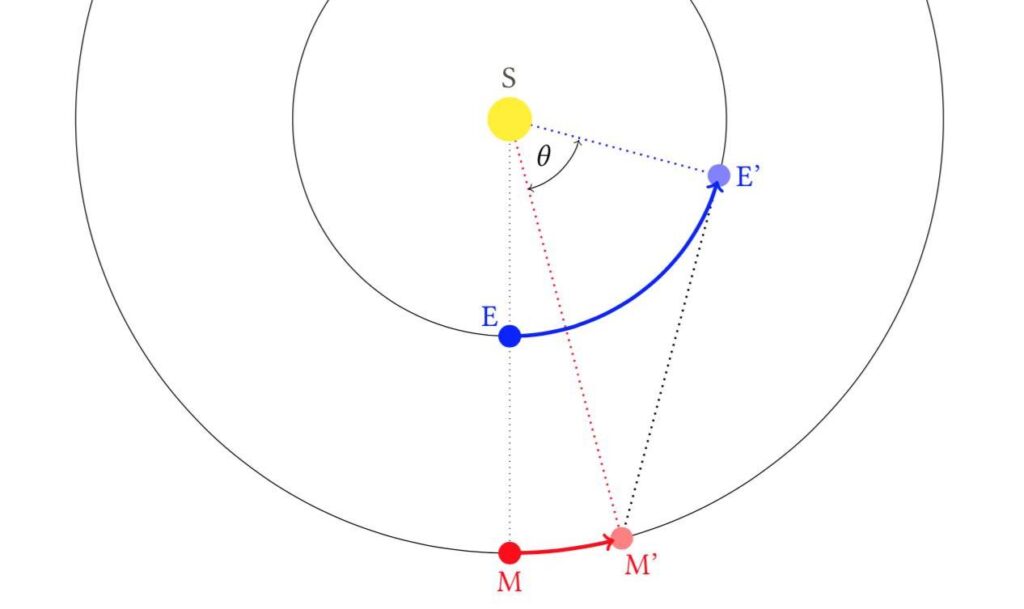
Initially, the Sun, Earth and Mars are all aligned. Here, Mars is at opposition at the point M. After some time \( t \), the Earth moves from E to E’, and Mars moves from M to M’. Mars at M’ is now at quadrature as the angle M’E’S is a right angle. The angle we need to determine is the angle E’SM’, denoted as \( \theta \) in the diagram. This is equal to Earth’s angular displacement minus Mars’ angular displacement \[ \theta = 2\pi\frac{t}{T_E} – 2\pi\frac{t}{T_M} = 2\pi t\left(\frac{1}{T_E} – \frac{1}{T_M}\right) \] where \( T_E \) and \( T_M \) denote Earth’s and Mars’ orbital periods respectively. The distance to Mars from the Sun is thus \[ r_M = \frac{r_\oplus}{\cos \theta} \] where, as usual, \( r_\oplus \) denotes Earth’s orbital radius. Thus Kepler was able to estimate the distances to all the planets as ratios of the Earth-Sun distance. Indeed, it wouldn’t be long someone observed a peculiar pattern. A pattern which meant that when Uranus and Neptune were discovered, one only had to measure their period to estimate their distance. How is this possible? Physics.

Universal Gravitation

It’s debated whether or not Newton actually was hit on the head by that apple, just as it’s debated whether or not he truly invented calculus. What he did do was show that the gravitational force between two objects was proportional to the product of their masses and inversely proportional to the square of the distance between them \[ F_g = \frac{GmM}{r^2} \] where the gravitational constant \( G \) is a very small proportionality constant. This is Newton’s Universal Law of Gravitation, a law which would remain mostly unchanged for several centuries until it was refined by Einstein’s theory of general relativity. Newton also developed three laws of motion, of which the second law states that the force acting on an object \( F \) is equal to the product of its mass and its acceleration, and the first states that objects will maintain a constant velocity unless acted upon by some net force. These two laws imply that anything moving in a circle must be subjected to a force directed radially inwards, and therefore must be accelerating.

Let’s consider a satellite of mass \( m \) orbiting a planet of mass \( M \). Treating everything as point masses, let \( r \) denote the radius of the satellite’s orbit. Suppose that the satellite’s orbit is circular, in which case its angular velocity \( \omega \) is equal to \( 2\pi / T \) where \( T \) is the period of the satellite’s orbit. Thus the centripetal force acting on the satellite is \[ F_c = mr\omega^2 = \frac{4\pi^2mr}{T^2} \] As the satellite is freely orbiting the planet, this centripetal force must be provided by gravity, and so we can equate this to \( F_g \): \[ \frac{4\pi^2mr}{T^2} = \frac{GmM}{r^2} \] Rearranging gives \[ \frac{T^2}{r^3} = \frac{4\pi^2}{GM} \] In other words, the period \( T \) is linearly related to the orbital radius \( r \) via \( T^2 \propto r^3 \). Even better, the mass of the satellite \( m \) cancels out. This is Kepler’s Third Law. All that’s needed is to measure the periods and distances to a few planets, then use these data points to calculate the linear coefficient \( 4\pi^2 / GM \), then extrapolate to new planets! And yes, this formula can also be used to estimate the mass of the Sun based on the orbital radii and orbital periods of the solar system planets. Kepler’s First and Second Laws address the nature of orbits; the first asserts that orbits are ellipses, with the Sun at one foci; the second law is to do with the conservation of angular momentum, in that a line drawn from the planet to the Sun will sweep equal areas during equal intervals of time. Intuitively, this means that an object in orbit will move fastest at periapsis (closest point), and slowest at apoapsis (furtherest point).

The empirical verification of Kepler’s Third Law, facilitated by the extensive observations made by Tycho Brahe at Uraniborg, is one of the great successes of early classical mechanics. It should be noted that the formula we derived above is based on circular orbits, however the change to the formula for the case of elliptical orbits is minor: the distance \( r \) is just replaced with the semi-major axis \( a \). All the distances Kepler used to derive his law were expressed as distance ratios relative to the Earth-Sun distance. For example, no one knew the actual distance to Jupiter, only that it was roughly 5.2 times the Earth-Sun distance. In order to truly narrow down these distances, astronomers needed extremely precise way to measure the distance from the Earth to the Sun. To do this, they had to wait for Venus to pass in front of the Sun.

The Transit of Venus

One of the rarest astronomical events in our Solar System is observing a transit of Venus. These occur in pairs 8 years apart, over a cycle that repeats every 243 years. The last transits of Venus occured on the 5/6 of June, 2012 and 8th of June, 2004. The most recent pair before that was 1874 and 1882, and we will have to wait till 2117 to wait for the next transit of Venus.

Observations of the transit are significantly important as they can be used to estimate the distance to the Sun with remarkable precision, far higher than Aristarchus’ geometric constructions outlined in Part 1. It is ostensibly the chief reason why James Cook sailed to the Pacific in 1769, though he also had secret orders to search for a mysterious continent. The idea, championed by Edmond Halley, was that if you could time how long it took Venus to complete its transit from different locations of Earth, you could apply the principles of parallax to calculate Earth’s distance from the Sun.

Illustration of the transit of Venus as observed from two locations on Earth. Credit: Wikimedia

Venus’ two paths across the Sun (as viewed from two locations) are essentially chords across the Sun’s face, so it’s possible to determine the angular separation between the two tracks based on the Sun’s angular diameter. In reality, this track separation is tiny, so a more accurate means of determining the distance is by timing the transits. This angle is essentially a parallax angle, so if we know the distance of the baseline (in this case the perpendicular distance between the observers) we can calculate the distance to Venus. If both observers on Earth are at antipodes, the baseline is simply the radius of the Earth. Let this baseline be \( b \) and assume we’ve measured some parallax angle \( \alpha \). Then the distance to Venus is \[ d_{EV} = \frac{b}{2\tan\left(\alpha/2\right)} = r_E – r_V\] However, we know that the distance of Venus from the Sun \( r_V \) is equal to some ratio \( m < 1 \) of the Earth-Sun distance \( r_E \), where \( m \) can be determined via the angle of greatest elongation method, or instead via Kepler’s Third Law. Thus \( d_{EV} = r_E(1 – m) \), and so \begin{align*} r_E = \frac{b}{2\tan\left(\alpha/2\right)\left(1-m\right)} \end{align*} The equation above is highly simplified and neglects many aspects of the transit, such as the effect of Earth’s rotation which can make the transit appear slightly longer or shorter depending on where the observer is located. Complicating matters is the black drop effect, making it impossible to tell exactly when a transit starts or finishes. Nevertheless, the transit of Venus was a significant improvement to Aristarchus’ method that we covered in Part 1, providing a state-of-the-art measurement of the distance from Earth to the Sun, and enabling astronomers – via Kepler’s Law – to infer the distance to all the known planets in our Solar System.

This work is licensed under a Creative Commons Attribution 4.0 International License.